PRO (category theory)

In category theory, a PRO is a strict monoidal category whose objects are the natural numbers (incl. zero), and whose tensor product is given on objects by the addition on numbers.

Some examples of PROs:

the discrete category 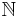$\mathbb{N}$ of natural numbers,
the category FinSet of natural numbers and functions between them,
the category Bij of natural numbers and bijections,
the category Inj of natural numbers and injections,
the simplicial category $\Delta$ of natural numbers and monotonic functions.

The name PRO is an abbreviation of "PROduct category". PROBs and PROPs are defined similarly with the additional requirement for the category to be braided, and to have a symmetry (that is, a permutation), respectively.

Algebras of a PRO

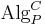An algebra of a PRO $P$ in a monoidal category $C$ is a strict monoidal functor from $P$ to $C$ . Every PRO $P$ and category $C$ give rise to a category $\mathrm{Alg}_P^C$ of algebras whose objects are the algebras of $P$ in $C$ and whose morphisms are the natural transformations between them.

For example:

an algebra of 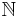$\mathbb{N}$ is just an object of $C$ ,
an algebra of FinSet is a commutative monoid object of $C$ ,
an algebra of $\Delta$ is a monoid object in $C$ .

More precisely, what we mean here by "the algebras of $\Delta$ in $C$ are the monoid objects in $C$ " for example is that the category of algebras of $P$ in $C$ is equivalent to the category of monoids in $C$ .

References

Saunders MacLane (1965). "Categorical Algebra". Bulletin of the American Mathematical Society 71: 40–106. doi:10.1090/S0002-9904-1965-11234-4.

Tom Leinster (2004). Higher Operads, Higher Categories. Cambridge University Press. http://www.maths.gla.ac.uk/~tl/book.html.

PRO (category theory)

Algebras of a PRO

See also

References